The single slit to the left of the two slits ensures that light reaching the two slits is from the same part of the source and therefore in phase. Note that a laser beam produces a coherent light source and can be used to create an interference pattern in the left configuration. Suggestion: To make the double slit, I used a thin metal pie tin (the disposable sort), and cut the slits with a utility knife with two blades mounted side-by-side. This made it easy to cut parallel slits, and by using paper spacers between the blades I could vary the width between the slits easily and get a variety to experiment with. Light - Light - Young's double-slit experiment: The observation of interference effects definitively indicates the presence of overlapping waves. Thomas Young postulated that light is a wave and is subject to the superposition principle; his great experimental achievement was to demonstrate the constructive and destructive interference of light (c. Single slit diffraction. In classical physics, we can classify optical phenomena into one of two categories: ray optics and wave optics. Light is a transverse electromagnetic wave. In many situations, the wavelengths of the light being studied are very small compared to the dimensions of the equipment used to study the light. Two-slit diffraction with single electrons, in which one measures the Coulomb field produced by the electrons at the far-away detector.
Learning Objectives
By the end of this section, you will be able to:
- Describe the combined effect of interference and diffraction with two slits, each with finite width
- Determine the relative intensities of interference fringes within a diffraction pattern
- Identify missing orders, if any
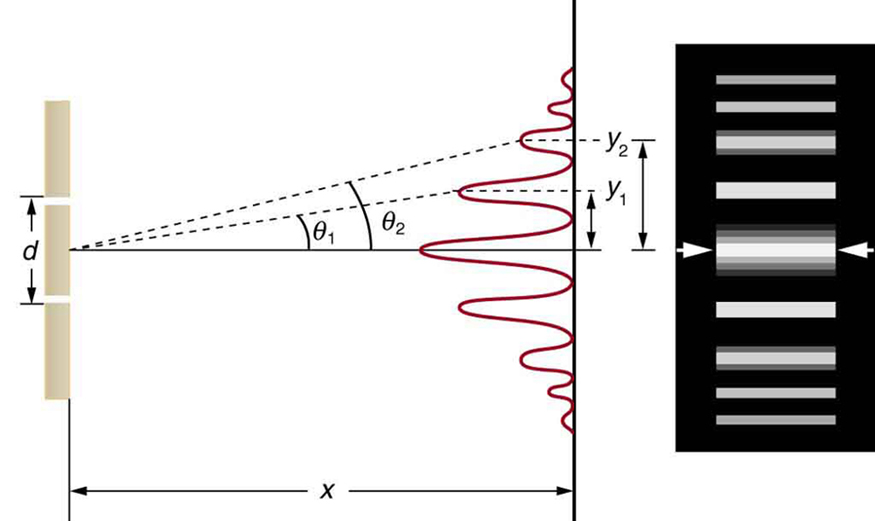
When we studied interference in Young's double-slit experiment, we ignored the diffraction effect in each slit. We assumed that the slits were so narrow that on the screen you saw only the interference of light from just two point sources. If the slit is smaller than the wavelength, then Figure 4.3.4a shows that there is just a spreading of light and no peaks or troughs on the screen. Therefore, it was reasonable to leave out the diffraction effect in that chapter. However, if you make the slit wider, Figure 4.3.4b and (c) show that you cannot ignore diffraction. In this section, we study the complications to the double-slit experiment that arise when you also need to take into account the diffraction effect of each slit.
To calculate the diffraction pattern for two (or any number of) slits, we need to generalize the method we just used for a single slit. That is, across each slit, we place a uniform distribution of point sources that radiate Huygens wavelets, and then we sum the wavelets from all the slits. This gives the intensity at any point on the screen. Although the details of that calculation can be complicated, the final result is quite simple:
Two-Slit Diffraction Pattern
The diffraction pattern of two slits of width (a) that are separated by a distance d is the interference pattern of two point sources separated by d multiplied by the diffraction pattern of a slit of width (a).
In other words, the locations of the interference fringes are given by the equation
Whatsapp signal telegram viber. [d , sin , theta = m lambda]
the same as when we considered the slits to be point sources, but the intensities of the fringes are now reduced by diffraction effects, according to Equation 4.3.11. [Note that in the chapter on interference, we wrote (d , sin , theta = m lambda) and used the integer (m) to refer to interference fringes. Equation 4.2.1 also uses (m), but this time to refer to diffraction minima. If both equations are used simultaneously, it is good practice to use a different variable (such as (n)) for one of these integers in order to keep them distinct.]
Interference and diffraction effects operate simultaneously and generally produce minima at different angles. This gives rise to a complicated pattern on the screen, in which some of the maxima of interference from the two slits are missing if the maximum of the interference is in the same direction as the minimum of the diffraction. We refer to such a missing peak as a missing order. One example of a diffraction pattern on the screen is shown in Figure (PageIndex{1}). The solid line with multiple peaks of various heights is the intensity observed on the screen. It is a product of the interference pattern of waves from separate slits and the diffraction of waves from within one slit.

Example (PageIndex{1}): Intensity of the Fringes
Figure (PageIndex{1}) shows that the intensity of the fringe for m=3 is zero, but what about the other fringes? Calculate the intensity for the fringe at m=1 relative to (I_0), the intensity of the central peak.
Strategy
Determine the angle for the double-slit interference fringe, using the equation from Interference, then determine the relative intensity in that direction due to diffraction by using Equation 4.3.11.
Solution
From the chapter on interference, we know that the bright interference fringes occur at (d , sin , theta = m lambda), or
[sin , theta = dfrac{mlambda}{d}.]
From Equation 4.3.11,
[I = I_0 left(dfrac{sin , beta}{beta}right)^2 nonumber]
where
Two Slit Diffraction
[beta = dfrac{phi}{2} = dfrac{pi a sin , theta}{lambda}. nonumber]
Substituting from above,
[beta = dfrac{pi a sin , theta}{lambda} = dfrac{pi a}{lambda} cdot dfrac{mlambda}{d} = dfrac{mpi a}{d}. nonumber]
For (a = 2lambda, , d = 6 lambda), and (m = 1), Nikon d600 shutter count limit.
[beta = dfrac{(1)pi (2lambda)}{(6 lambda)} = dfrac{pi}{3}. nonumber]
Then, the intensity is
[I = I_0 left(dfrac{sin , beta}{beta}right)^2 = I_0 left(dfrac{sin , (pi/3)}{pi/3}right)^2 = 0.684 I_0. nonumber]
Significance
Note that this approach is relatively straightforward and gives a result that is almost exactly the same as the more complicated analysis using phasors to work out the intensity values of the double-slit interference (thin line in Figure (PageIndex{1})). The phasor approach accounts for the downward slope in the diffraction intensity (blue line) so that the peak near m=1 occurs at a value of θ ever so slightly smaller than we have shown here.
Example (PageIndex{2}): Two-Slit Diffraction
Suppose that in Young's experiment, slits of width 0.020 mm are separated by 0.20 mm. If the slits are illuminated by monochromatic light of wavelength 500 nm, how many bright fringes are observed in the central peak of the diffraction pattern?
Solution
From Equation 4.2.1, the angular position of the first diffraction minimum is (theta approx sin , theta = dfrac{lambda}{a} = dfrac{5.0 times 10^{-7}m}{2.0 times 10^{-5}m} = 2.5 times 10^{-2} rad).
Using (d sin , theta = m lambda) for (theta = 2.5 times 10^{-2} rad), we find
[m = dfrac{d , sin , theta}{lambda} = dfrac{(0.20 , mm)(2.5 times 10^{-2} rad)}{(5.0 times 10^{-7}m)} = 10, nonumber]
which is the maximum interference order that fits inside the central peak. We note that (m=±10) are missing orders as (θ) matches exactly. Accordingly, we observe bright fringes for
m = −9, −8, −7, −6, −5, −4, −3, −2, −1, 0, +1, +2, +3, +4, +5, +6, +7, +8, and +9
for a total of 19 bright fringes.
Exercise (PageIndex{1})
For the experiment in Example (PageIndex{2}), show that m=20 is also a missing order.
Solution
From (d , sin , theta = mlambda), the interference maximum occurs at (2.87^o) for (m = 20). From Equation 4.2.1, this is also the angle for the second diffraction minimum. (Note: Both equations use the index m but they refer to separate phenomena.)
Two Slit Diffraction Pattern
Explore the effects of double-slit diffraction. In this simulation written by Fu-Kwun Hwang, select N=2 using the slider and see what happens when you control the slit width, slit separation and the wavelength. Can you make an order go 'missing?'
Contributors and Attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Do not show again
In this Demonstration we visualize the diffraction pattern of equally spaced slits of equal width, also known as a diffraction grating. It can be shown that the diffraction pattern is equivalent to the diffraction pattern for delta function slits modulated by the diffraction pattern of a single slit of finite width. The latter thus acts as an envelope, shown by the thick dashed line. Special cases of this system include the single () and double () slits, which appear in introductory physics courses. The horizontal scale is arbitrary and the vertical scale normalized to the peak intensity.
Contributed by: Peter Falloon(March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For an array of slits of width and equal spacing , the intensity of the diffracted light on a screen may be neatly expressed as
,
where is the peak intensity and is the Chebyshev polynomial of the second kind, which appears when we simplify the ratio .
The parameter is a normalized wavenumber. It is related to the actual wavenumber , the perpendicular distance from the diffraction grating to the screen on which the pattern is observed, and the distance from the center of the pattern , by .
The formula for the intensity is valid within the Fraunhofer diffraction regime, for which . In this case, the diffraction pattern is equivalent to the Fourier transform of the diffraction grating. This explains why, since an array of finite-width slits is equivalent to the convolution of an array of delta function slits with a single slit, the resulting diffraction pattern is the product of the two corresponding diffraction patterns.
Painting fashion. Snapshot 1: for a single, infinitely narrow slit, the diffraction pattern is constant; this is essentially because the Fourier transform of the delta function is constant
Snapshot 2: for multiple infinitely narrow slits, there is an infinitely repeating pattern of peaks and troughs, corresponding to constructive/destructive interference between paths from different slits

Example (PageIndex{1}): Intensity of the Fringes
Figure (PageIndex{1}) shows that the intensity of the fringe for m=3 is zero, but what about the other fringes? Calculate the intensity for the fringe at m=1 relative to (I_0), the intensity of the central peak.
Strategy
Determine the angle for the double-slit interference fringe, using the equation from Interference, then determine the relative intensity in that direction due to diffraction by using Equation 4.3.11.
Solution
From the chapter on interference, we know that the bright interference fringes occur at (d , sin , theta = m lambda), or
[sin , theta = dfrac{mlambda}{d}.]
From Equation 4.3.11,
[I = I_0 left(dfrac{sin , beta}{beta}right)^2 nonumber]
where
Two Slit Diffraction
[beta = dfrac{phi}{2} = dfrac{pi a sin , theta}{lambda}. nonumber]
Substituting from above,
[beta = dfrac{pi a sin , theta}{lambda} = dfrac{pi a}{lambda} cdot dfrac{mlambda}{d} = dfrac{mpi a}{d}. nonumber]
For (a = 2lambda, , d = 6 lambda), and (m = 1), Nikon d600 shutter count limit.
[beta = dfrac{(1)pi (2lambda)}{(6 lambda)} = dfrac{pi}{3}. nonumber]
Then, the intensity is
[I = I_0 left(dfrac{sin , beta}{beta}right)^2 = I_0 left(dfrac{sin , (pi/3)}{pi/3}right)^2 = 0.684 I_0. nonumber]
Significance
Note that this approach is relatively straightforward and gives a result that is almost exactly the same as the more complicated analysis using phasors to work out the intensity values of the double-slit interference (thin line in Figure (PageIndex{1})). The phasor approach accounts for the downward slope in the diffraction intensity (blue line) so that the peak near m=1 occurs at a value of θ ever so slightly smaller than we have shown here.
Example (PageIndex{2}): Two-Slit Diffraction
Suppose that in Young's experiment, slits of width 0.020 mm are separated by 0.20 mm. If the slits are illuminated by monochromatic light of wavelength 500 nm, how many bright fringes are observed in the central peak of the diffraction pattern?
Solution
From Equation 4.2.1, the angular position of the first diffraction minimum is (theta approx sin , theta = dfrac{lambda}{a} = dfrac{5.0 times 10^{-7}m}{2.0 times 10^{-5}m} = 2.5 times 10^{-2} rad).
Using (d sin , theta = m lambda) for (theta = 2.5 times 10^{-2} rad), we find
[m = dfrac{d , sin , theta}{lambda} = dfrac{(0.20 , mm)(2.5 times 10^{-2} rad)}{(5.0 times 10^{-7}m)} = 10, nonumber]
which is the maximum interference order that fits inside the central peak. We note that (m=±10) are missing orders as (θ) matches exactly. Accordingly, we observe bright fringes for
m = −9, −8, −7, −6, −5, −4, −3, −2, −1, 0, +1, +2, +3, +4, +5, +6, +7, +8, and +9
for a total of 19 bright fringes.
Exercise (PageIndex{1})
For the experiment in Example (PageIndex{2}), show that m=20 is also a missing order.
Solution
From (d , sin , theta = mlambda), the interference maximum occurs at (2.87^o) for (m = 20). From Equation 4.2.1, this is also the angle for the second diffraction minimum. (Note: Both equations use the index m but they refer to separate phenomena.)
Two Slit Diffraction Pattern
Explore the effects of double-slit diffraction. In this simulation written by Fu-Kwun Hwang, select N=2 using the slider and see what happens when you control the slit width, slit separation and the wavelength. Can you make an order go 'missing?'
Contributors and Attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Do not show again
In this Demonstration we visualize the diffraction pattern of equally spaced slits of equal width, also known as a diffraction grating. It can be shown that the diffraction pattern is equivalent to the diffraction pattern for delta function slits modulated by the diffraction pattern of a single slit of finite width. The latter thus acts as an envelope, shown by the thick dashed line. Special cases of this system include the single () and double () slits, which appear in introductory physics courses. The horizontal scale is arbitrary and the vertical scale normalized to the peak intensity.
Contributed by: Peter Falloon(March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For an array of slits of width and equal spacing , the intensity of the diffracted light on a screen may be neatly expressed as
,
where is the peak intensity and is the Chebyshev polynomial of the second kind, which appears when we simplify the ratio .
The parameter is a normalized wavenumber. It is related to the actual wavenumber , the perpendicular distance from the diffraction grating to the screen on which the pattern is observed, and the distance from the center of the pattern , by .
The formula for the intensity is valid within the Fraunhofer diffraction regime, for which . In this case, the diffraction pattern is equivalent to the Fourier transform of the diffraction grating. This explains why, since an array of finite-width slits is equivalent to the convolution of an array of delta function slits with a single slit, the resulting diffraction pattern is the product of the two corresponding diffraction patterns.
Painting fashion. Snapshot 1: for a single, infinitely narrow slit, the diffraction pattern is constant; this is essentially because the Fourier transform of the delta function is constant
Snapshot 2: for multiple infinitely narrow slits, there is an infinitely repeating pattern of peaks and troughs, corresponding to constructive/destructive interference between paths from different slits
Snapshot 3: for a single slit of finite width, the diffraction pattern has the well-known form of a sinc function
Snapshot 4: for multiple slits of finite width, the diffraction is a pattern of peaks and troughs modulated by the sinc function pattern arising from the finite width of each slit
Related Links
- Diffraction Grating (Wolfram ScienceWorld)
- Fraunhofer Diffraction (Wolfram ScienceWorld)
- Fraunhofer Diffraction—Single Slit (Wolfram ScienceWorld)
- Fraunhofer Diffraction—Double Slit (Wolfram ScienceWorld)

